本经验介绍函数的单调性概念,基本函数的单调性归纳、函数单调性的主要性质和判断求解函数的单调情况或单调区间。
工具/原料
高中数学基本知识
导数有关知识
一.单调性的定义
1、 函数的单调性也可以叫做函数的增减性。当函数 f(x) 的自变量在其定义区间内增大(或减小)时,函数值f(x)也随着增大(或减小),则称该函数为在该区间上具有单调性。

2、 在定义域范围内的某个区间D上,当自变量增加而函数值随之减小,则称之为单调增函数,反之称之为单调减函数。增函数的图象是上升的,减函数的图象是下降的。单调增函数和单调减函数统称为单调函数。
3、 不是所有函数都是单调函数。如果说该函数f(x)在某个区间D上具有单调性,则将区间D称作函数的一个单调区间。
4、 对单调性的函数而言,它可能只有一个或多个单调增区间,也可能只有一个或多个单调减区间,还可能既有一个或多个单调增区间和单调减区间。
二.基本函数的单调性及单调区间
1、 1.常数函数y=C,不是单调函数,没有单调区间。
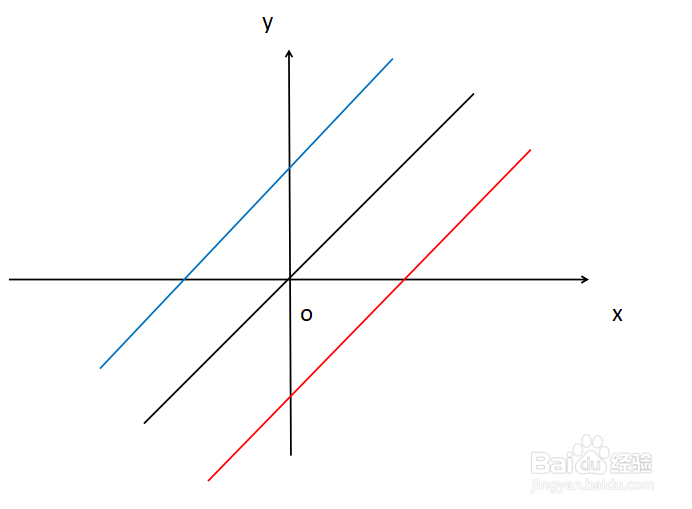
2、 2.一次函数y=ax+b(a≠0)定义域为R,是单调函数,单调性取决于a的正负。当a>0时为单调增函数,单调增区间为(-∞,+∞);当a<0时为单调减函数,单调减区间为(-∞,+∞)。

3、 3.二次函数y=ax^2+bx+c(a≠0)定义域为R,具有单调性,有单调区间,取决于a的正负和对称x0=-b/2a的值。当a>0时,区间(-∞,-b/2a)上为单调减区间,(-b/2a,+∞)上为单调增区间;当a<0时,区间(-∞,-b/2a)上为单调增区间,(-b/2a,+∞)上为单调减区间。
4、 4.幂函数y=x^a,其单调性要根据a的取值来讨论。如a=2时,y=x^2是二次函数的一种情形,单调性符合二次函数性质;当a=3时,y=x^3则在整个实数范围内为单调增函数,单调增区间即为(-∞,+∞)。
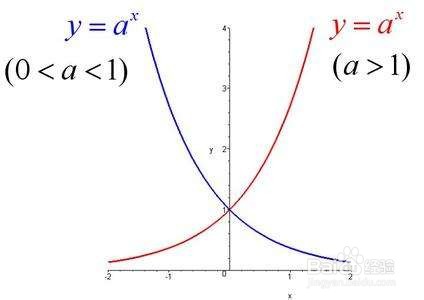
5、 5.指数函数y=a^x(a>0且a≠1)定义域为R,其单调性取决于a的取值。当a>1时,则指数函数单调递增;若0<a<1,则为单调递减。
6、 6.对数函数y=loga(x)(a>0且a≠1)定义域为定义域是(0,+∞),单调性取决于a的取值。当a>1时,在定义域上为单调增函数;当0<a<1时,在定义域上为单调减函数。

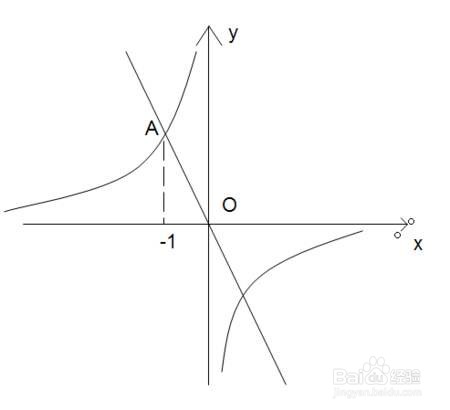
7、 7.反比例函数y=k/x(k≠0)定义域要求x≠0,其单调性取决于k的正负。当k>0时,函数在(-∞,0),(0,+∞)上同为减函数;当k<0时,函数在(-∞,0),(0,+∞)上同为增函数。

8、 8.三角函数类型比较多,如正弦函数y=sinx、余弦函数y=cosx、正切函数y=tanx、余切函数y=ctgx、正割函数y=secx、余割函数y=cscx、正矢函数versinx=1-cosx、余矢函数coversinx=1-sinx、半正矢函数haversinx=(1-cosx)/2、半余矢函数hacoversinx=(1-sinx)/2、外正割函数exsecx=secx-1等。前四种常见三角函数的单调性如下:
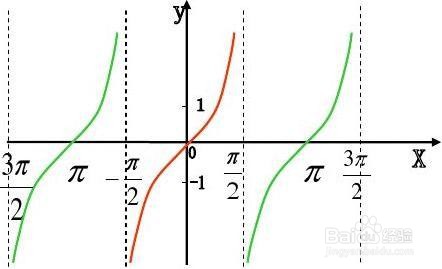
9、对于y=sinx,增区间为[2kπ-π/2,2kπ+π/2],减区间为[2kπ+π/2,2kπ+3π/2]。对于y=cosx,增区间为[2kπ-π,2kπ],减区间为[2kπ,2kπ+π]。对于y=tanx,增区间为[kπ-π/2,kπ+π/2]。对于y=ctgx,减区间为[kπ,kπ+π],以上k∈Z。
三、函数单调性的性质
1、 1.f(x)与f(x)+C(C为任意常数)具有相同单调性;
2、 2.f(x)与 g(x) = C*f(x)在 C>0 时有相同单调性,当 C<0 时,具有相反单调性;
3、 3.当f(x)、g(x)都是增函数时,若两者都恒大于零,则f(x)×g(x)为增函数;若两者都恒小于零,则为减函数;
4、 4.当f(x)、g(x)都是减函数时,若两者都恒大于零,则f(x)×g(x)为减函数;若两者都恒小于零,则为增函数;
5、 5.两个增函数之和仍为增函数,如y=x^2+2^x;增函数减去减函数为增函数,如y=x^2-2^(-x);
6、 6.两个减函数之和仍为减函数;减函数减去增函数为减函数;函数值在区间内同号时, 增(减)函数的倒数为减(增)函数。
7、 7.对复合函数y=f[g(x)]的定义域内,令u=g(x),则y=f[g(x)]的单调性由u=g(x)与y=f(x)的单调性共同确定,并符合“同增异减”判断规律。

四、函数单调性的判断
1、定义法根据函数单调性的定义,判断函数单调的步骤为:①在区间D上,任取x1,x2,不妨令x1<x2;②作差f(x2)-f(x1);③对f(x2)-f(x1)的结果进行变形处理(通常是配方、因式分解、有理化、通分,利用公式等等方法);④确定符号f(x2)-f(x1)的正负;⑤下结论,若f(x2)-f(x1)>0,则为增函数,该区间D为增区间;若f(x2)-f(x1)<0,则为减函数,区间D为减区间。

3、导数法如果函数y=f(x)在区间D内可导,若x∈D时恒有f'(x)>0,则函数y=f(x)在区间D内单调增加;反之,若x∈D时,f'(x)<0,则称函数y=f(x)在区间D内单调减少。

5、 对于上述两种方法,定义法一般主要用于判断或证明,导数法不仅可以判断函数的单调性,还可以求解函数的单调区间。导数是求解函数单调区间的重要方法。
