1、从定义出发,奇函数:定义域关于骒貉缭塄原点对称的函数f(x),满足在定义内任意f(x)都有 f(x)=-f(-x)。偶函数:定义域关于原点对称的函数f(x),满足在定义内任意f(x)都有 f(x)=f(-x)。
2、首先列举三个不同的函数进行举例,先观察定义域,再判断是否满足定义要求。
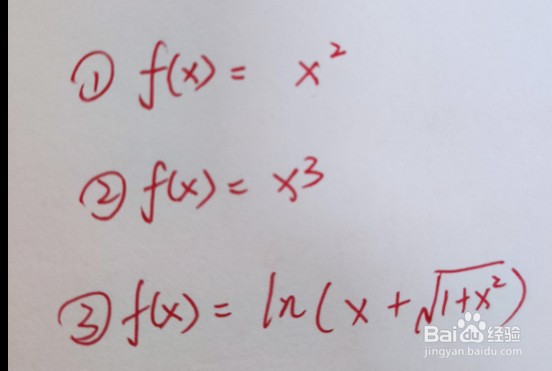
3、第一步,观察三个函数的定义域,满足x都属于R,所以其定义域是对称的,【如果函数的定义域一个是正半轴是(1,2),负半轴是(-3,-2)那么定义域就是不对称的】。第二步,将-x带入函数,计算f(旌忭檀挢x)与f(-x)二者的关系,如果相等就是偶函数,互为相反数则为奇函数。【图中为求解过程】

