1、首先,由题意可以联想到基本不等式:a²+b²≥2ab,b²+c²≥2bc,a²+c²≥2ac。将上式相加会得到新条件:a²+b²+c²≥ab+bc+ac。即:
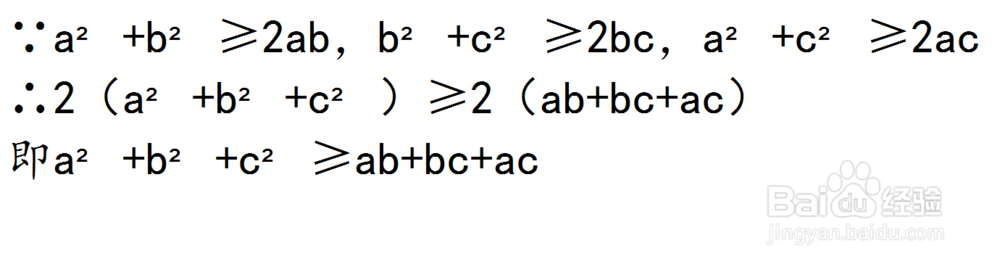
2、那么,看到a²+b²+c²这样的式子,我尺攵跋赈们显然会想到完全平方公式——(a+b+c)²=a²+b²+c²+2ab+2bc+2ac。既然知道上式中的一部分大于等于某个值,那么,我们就可以联立二式,得到(a+b+c)²≥3ab+3bc+3ac。又因为a+b+c=1,那么ab+bc+ac≤1/3。即:

3、从上一步可以看出,我们要证明的式子中的a²+b²+c²,必然会和ab+bc+ac有关,所以对此式进行处理:-2(ab+bc+ac)≥-2/3。那么问题就很简单了,只要把(a+b+c)²展开并代入条件就可以得证了。即:

