三角形中位线的证明是初中的一个重要定理，也是许多学生要突破的重难点。
三角形的中位线定理
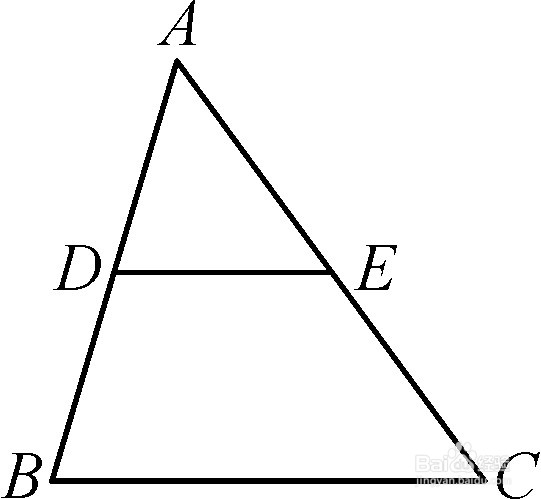
1、三角形的中位线平行于第三边（不与中位线接触），并且等于第三边的一半。如下图所示，在三角形ABC中，DE是以BC为底的三角形中位线，则可得DE//BC，且DE=BC/2。
三角形中位线证明
1、方法一：欲证DE=BC/2这种线段的倍半问题,往往可以将短的线段放大,转化为证明两线段相等,此题可将线段DE延长一倍至F,再连FC,把问题转化为证明四边形DFCB为平行四边吾疣璨普形.过C作AB的平行线交DE的延长线于F点。∵CF∥AD∴∠A=∠ACG∵∠AED=∠CEF、AE=CE、∠A=∠ACF∴△ADE≌△CFE(S.A.S)∴AD=CF(全等三角形对应边相等)∵D为AB中点∴AD=BD∴BD=CF又∵BD∥CF∴BCFD是平行四边形（一组对边平行且相等的四边形是平行四边形）∴DF∥BC且DF=BC∴DE=DF/2=BC/2∴DE为三角形ABC的中位线.
2、方法二：相似法：八年级下册第四章已学习过相似图形,也可以利用相似三角形的知识来解决.∵D是AB中点∴AD：AB=1：2∵E是AC中点∴AE：AC=1:2又∵∠A=∠A∴△ADE∽△ABC(S.A.S)∴AD：AB=AE：AC=DE：BC=1：2∠ADE=∠B，∠AED=∠C∴BC=2DE,BC∥DE
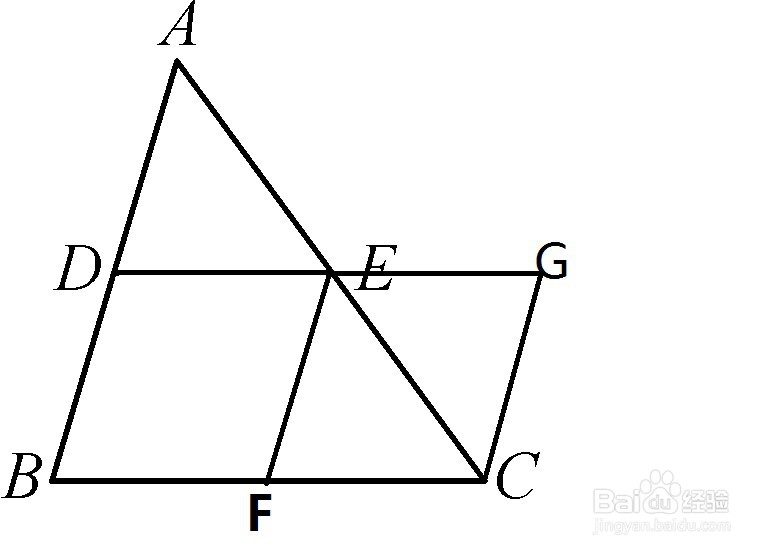
3、方法三：用截长补短的方法构造全等三角形,再证出平行四边形,得出结论.延长DE到点G，使EG=DE，连接CG∵点E是AC中点∴AE=CE∵AE=CE、鹳帕鄯区∠AED=∠CEG、DE=GE∴△ADE≌△CGE (S.A.S)∴AD=CG、∠G=∠ADE∵D为AB中点∴AD=BD∴BD=CG∵点D在边AB上∴DB∥CG∴BCGD是平行四边形∴DE=DG/2=BC/2∴所以DE为三角形ABC的中位线
