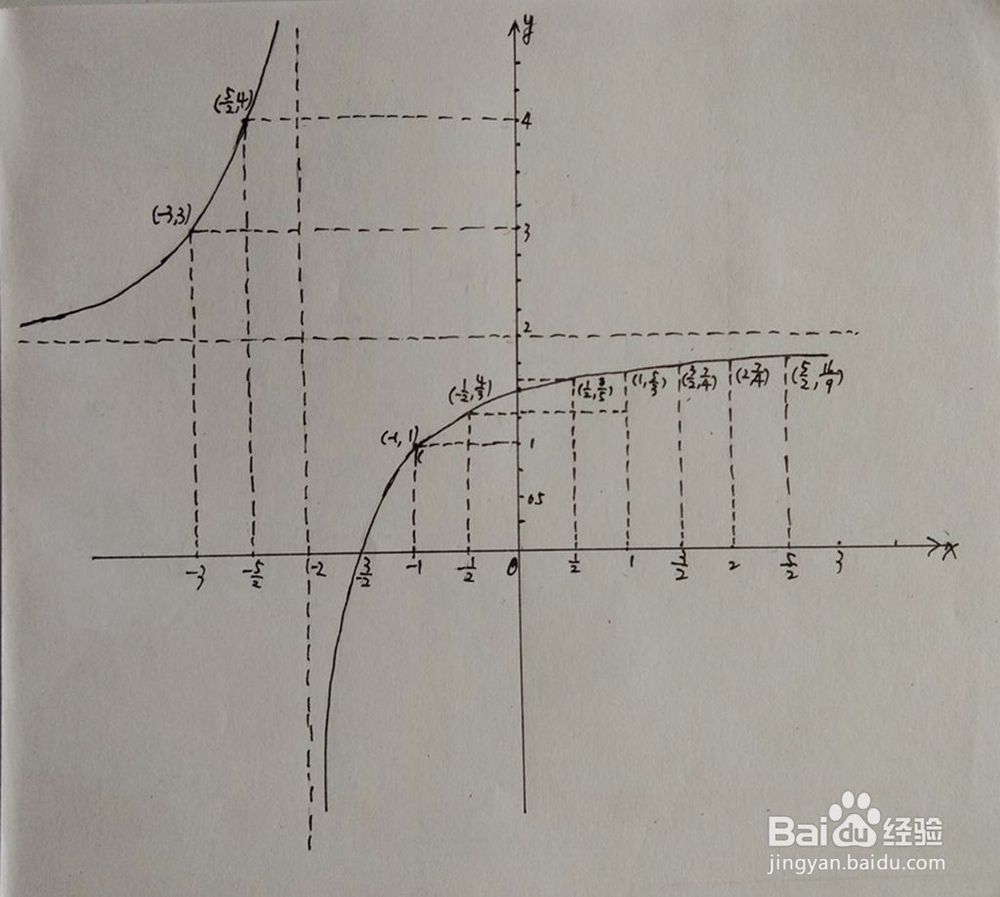
本经验,通过函数的定义域、值域、单调性、凸凹性等性质,介绍简要画出函数y=(2x+3)/(x+2)图像的基本步骤。
工具/原料
函数的基本性质
导数与单调性及凸凹关系
1.函数的定义域
1、y=(2x+3)/(x+2)的定义域:
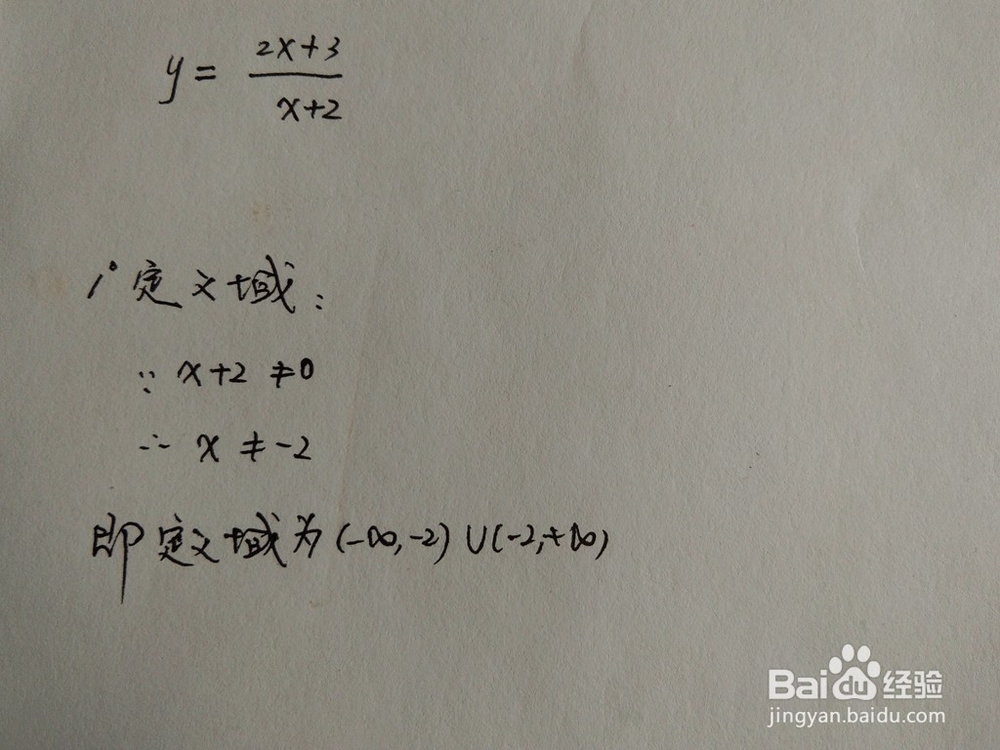
2.函数的单调性
1、通过导数,研究y=(2x+3)/(x+2)的单调性:
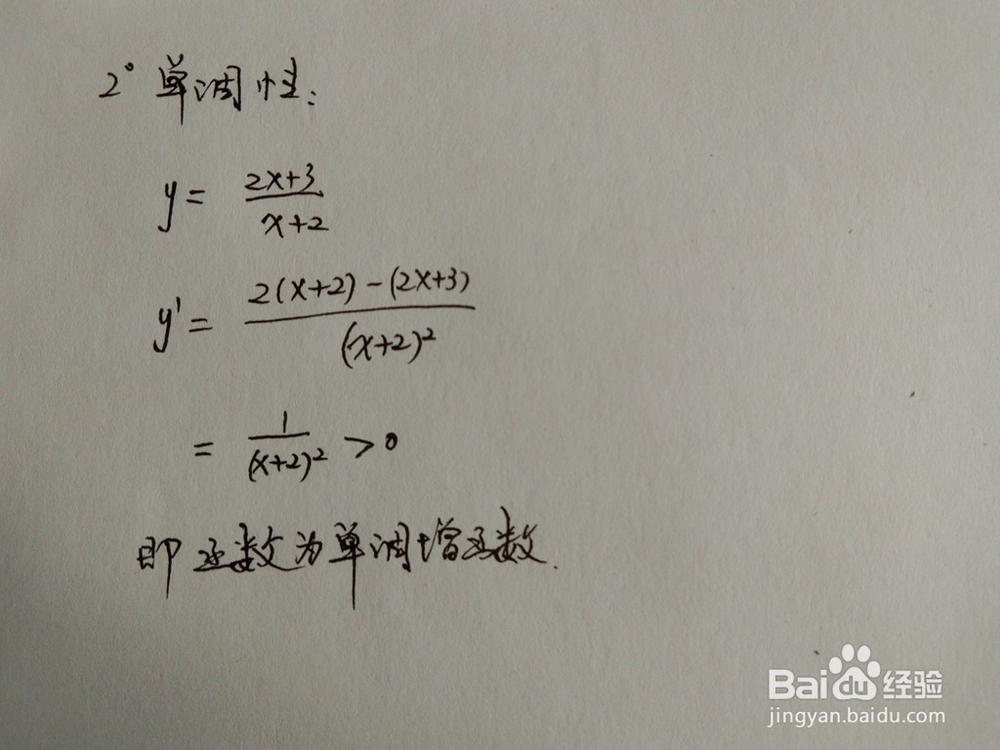
3.函数的值域问题
1、y=(2x+3)/(x+2)函数的值域如下:
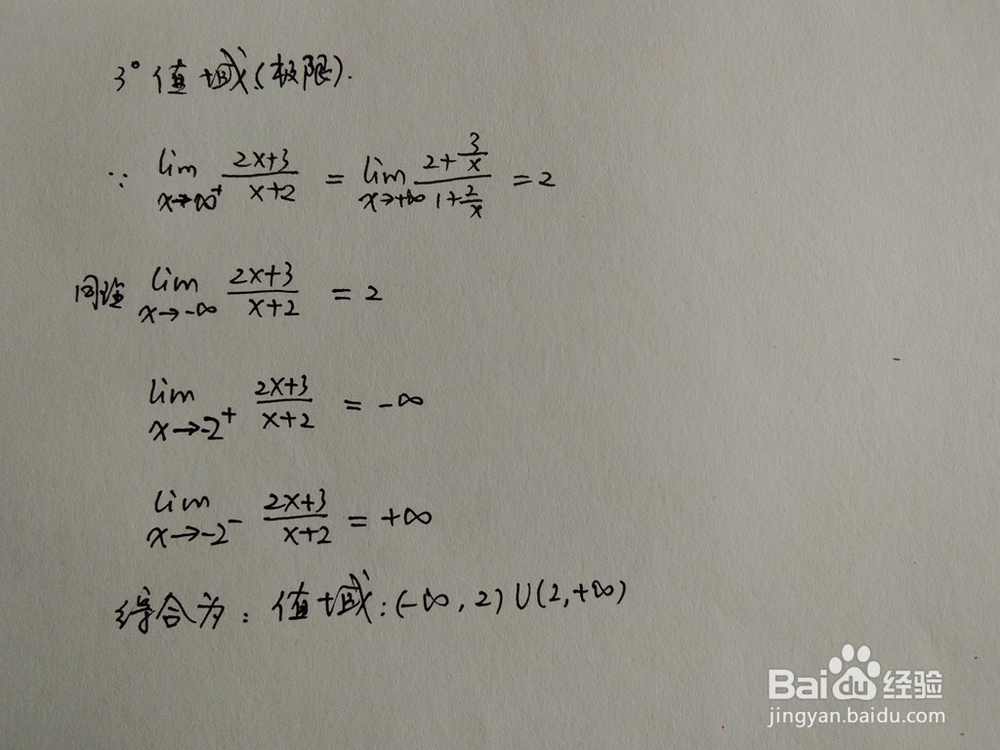
4.函数的凸凹问题
1、求函数y=(2x+3)/(x+2)的二阶导数,研究函数的凸凹性质如下:

5.函数上部分点解析图
1、当x=0,1/2,1,3/2,2,5/2时,求y值,坐标解析表如下:
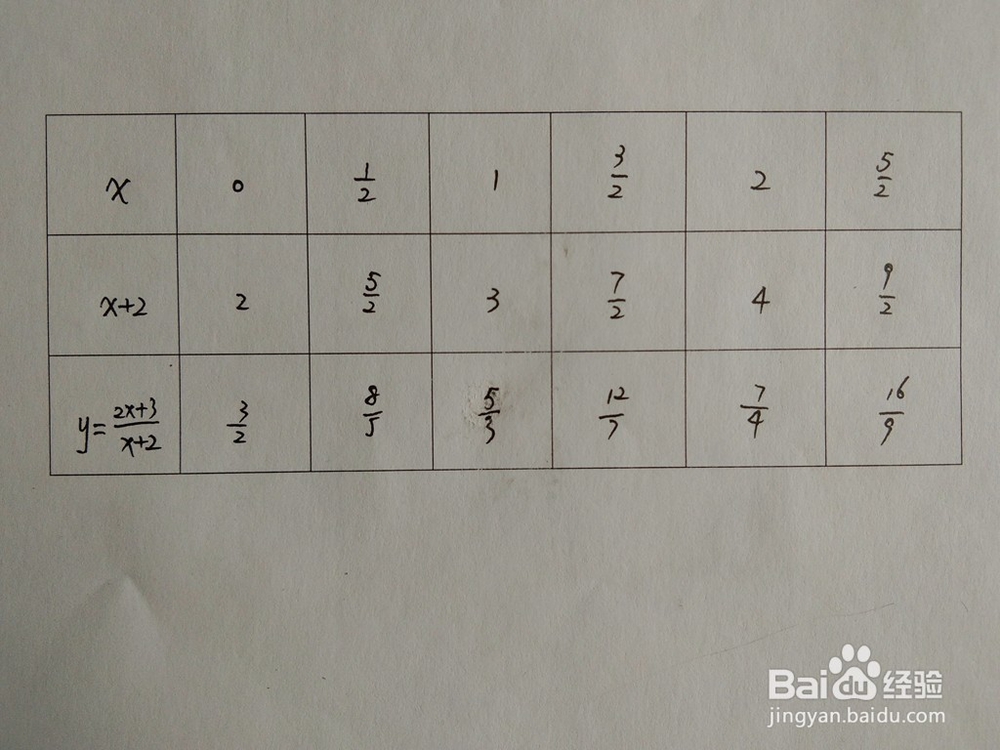
2、当x=-1/2,-1,-3/2,-2,-5/2,-3时,求y值,坐标解析表如下:
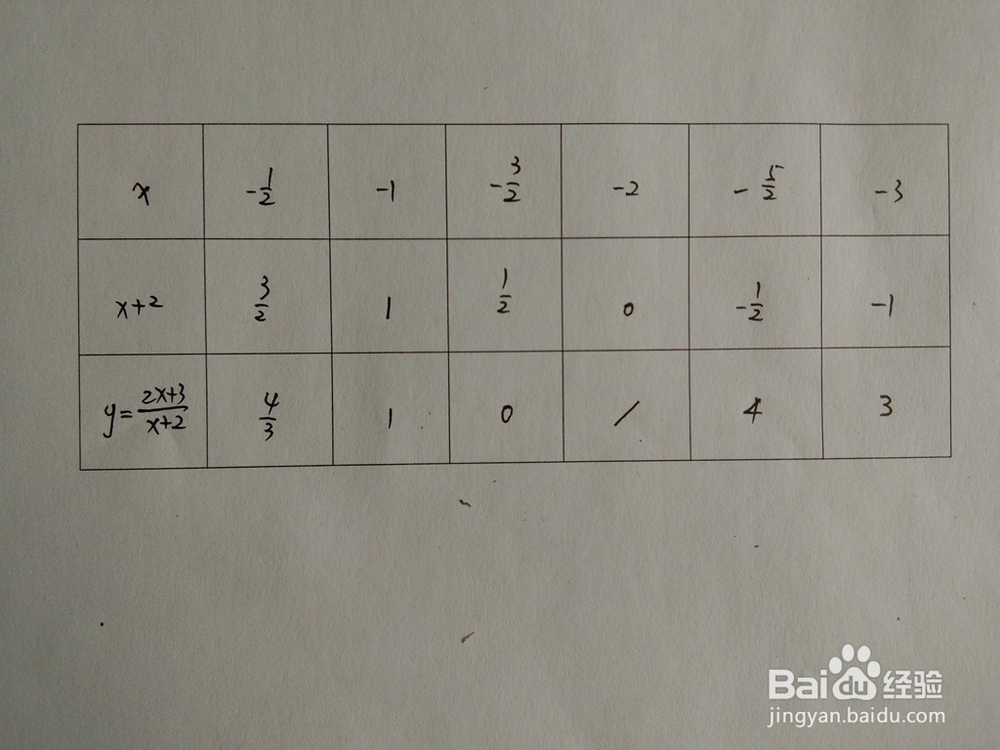
6.函数的示意图
1、y=(2x+3)/(x+2)函数的示意图如下: