拉格朗日中值定理有一个变形,即所谓的有限增量公式:f(x0+Δx)-f(x0)=f'(x0+θΔx)Δx,0<θ<1。其中的θ有一个很重要的性质:
若f(x)的二阶导在x0点连续,且不等于0,则
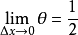
证明如下:
由于f''(x)在x0点连续,所以有
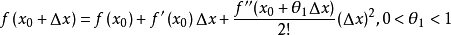
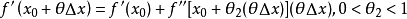
同时代入有限增量公式,可得
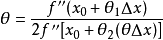
利用f"(x)在x0点处的连续性及f"(x0)≠0,在等式两边同取极限(令Δx趋于0),即可得结论。
扩展资料:
拉格朗日中值定理的运动学意义
对于曲线运动在任意一个运动过程中至少存在一个位置(或一个时刻)的瞬时速率等于这个过程中的平均速率。
拉格朗日中值定理在柯西的微积分理论系统中占有重要的地位。可利用拉格朗日中值定理对洛必达法则进行严格的证明,并研究泰勒公式的余项。从柯西起,微分中值定理就成为研究函数的重要工具和微分学的重要组成部分。
