理由如下:
一般情况下,如果将树的结点从上到下,每一层从左到右从1开始挨个编号,那么结点 i 的左孩子就是2i,右孩子就是2i+1,将这个规律反映到顺序存储中。
我们可以根据数组的下标i也能找到左孩子(2i)和右孩子(2I+1),前提是数组下标 i=0位丢弃不用,从i=1开始存储树的编号为1的根结点,以此类推。
所以,这样即使是将一棵树顺序存储到了一个一维数组中,结点 i 的左孩子就是2i,右孩子就是2i+1这套公式照样能够使用。
假设现在一棵非完全二叉树,拿一棵普通的二叉树举例,一棵普通二叉树有5种形态(空树、只有根结点、只有左子树、只有右子树、左右子树都有),从形态上来看是一棵“残缺不全”的二叉树。
如果从根结点开始从1 挨个编号,然后在存进一维数组中,那么有些结点可能没有孩子,那么它原本的孩子在数组中的位置就会被后面上来的的结点占据,这样在数组中再拿着2i或者2I+1找到的结点就不是实际情况下树中结点的左右孩子(实际情况下树中该结点可能甚至都没有孩子)。
因此,之所以说顺序存储只适用于完全二叉树,就是为了保证在一维数组中仍旧能够根据2i和2i+1去找左右孩子。
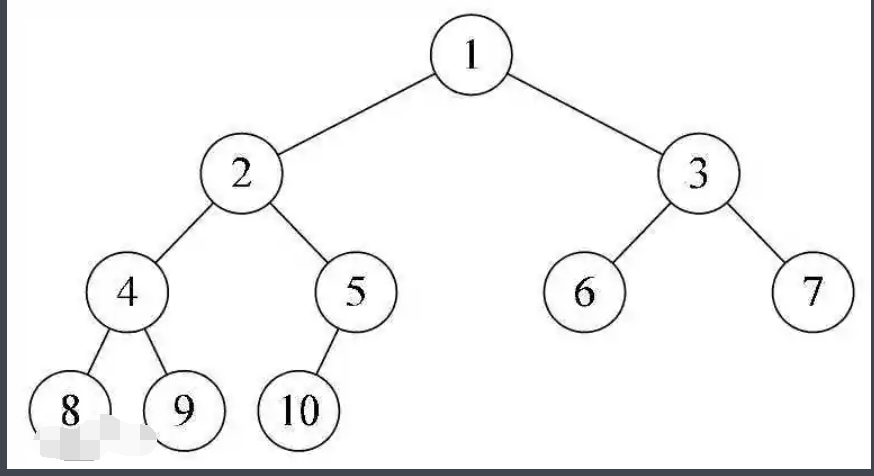
完全二叉树的特点:叶子结点只能出现在最下层和次下层,且最下层的叶子结点集中在树的左部。需要注意的是,满二叉树肯定是完全二叉树,而完全二叉树不一定是满二叉树。
性质
1、具有n个结点的完全二叉树的深度。
(注:[ ]表示向下取整)
2、如果对一棵有n个结点的完全二叉树的结点按层序编号, 则对任一结点i (1≤i≤n) 有:
如果i=1, 则结点i是二叉树的根, 无双亲;如果i>1, 则其双亲parent (i) 是结点[i/2]。
如果2i>n, 则结点i无左孩子, 否则其左孩子lchild (i) 是结点2i。
如果2i+1>n, 则结点i无右孩子, 否则其右孩子rchild (i) 是结点2i+1。
