1、根据函数的特征,含有分式则分母不为0,即定义域为非零实数。
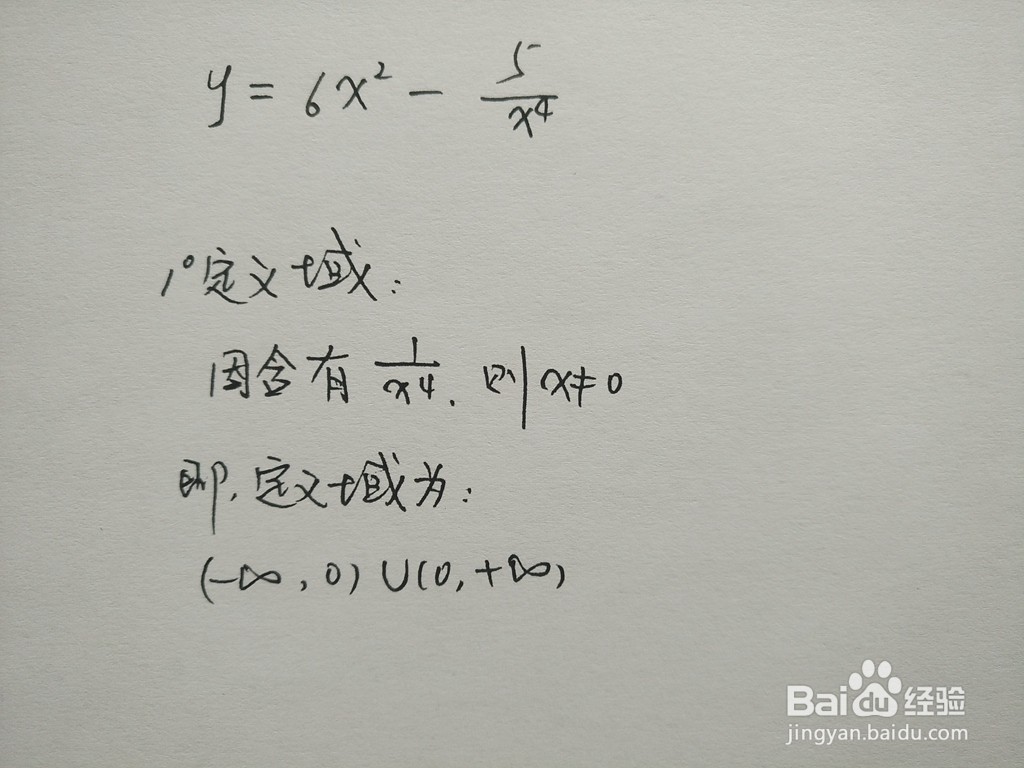
2、计算函数的一阶导数,求出函数驻点,由一阶导数的正负,判断函数的单调性,进而得到函数的单调区间。

3、函数的单调性也叫函数的增减性。当函数 f(x) 的自变量在其定义区间内增大(或减小)时,函数值f(x)也随着增大(或减小),则称该函数为在该区间上具有单调性。
4、函数的凸凹性:通过函数的二阶导数,得函数的拐点,再根据二阶导数的符号,判断函数的凸凹性,进而解析函数的凸凹区间。

5、根据偶函数的判断公式f(-x)=f(x),可以判断函数为偶函数,具体步骤如下。

6、函数的在无穷处的极限:
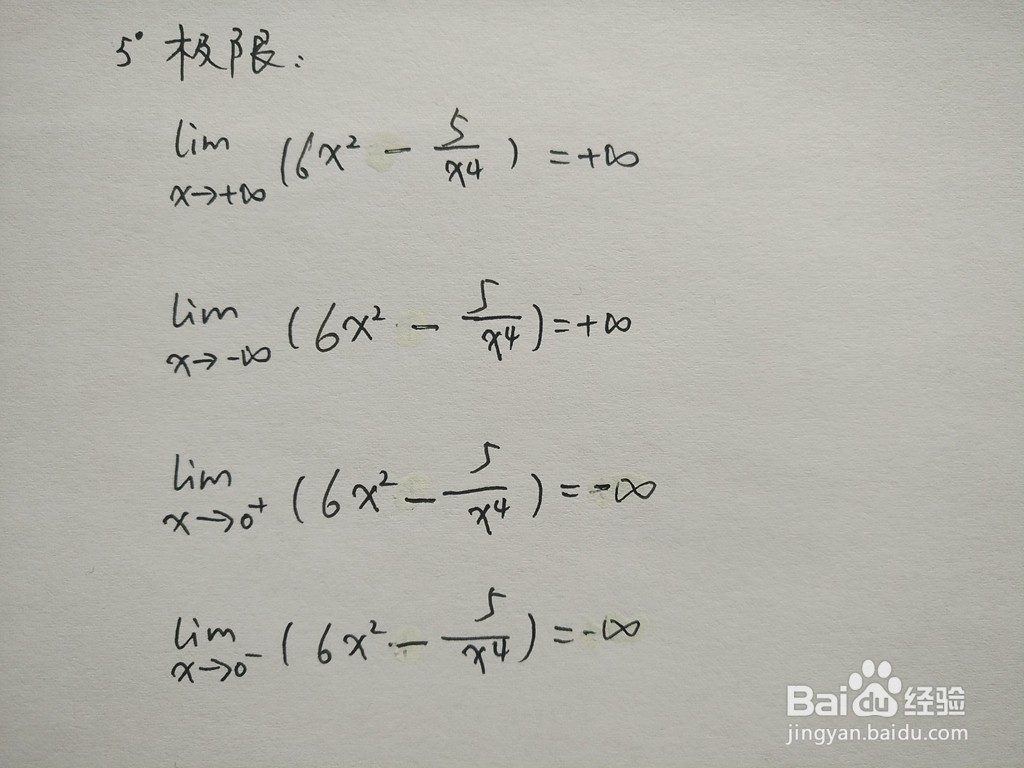
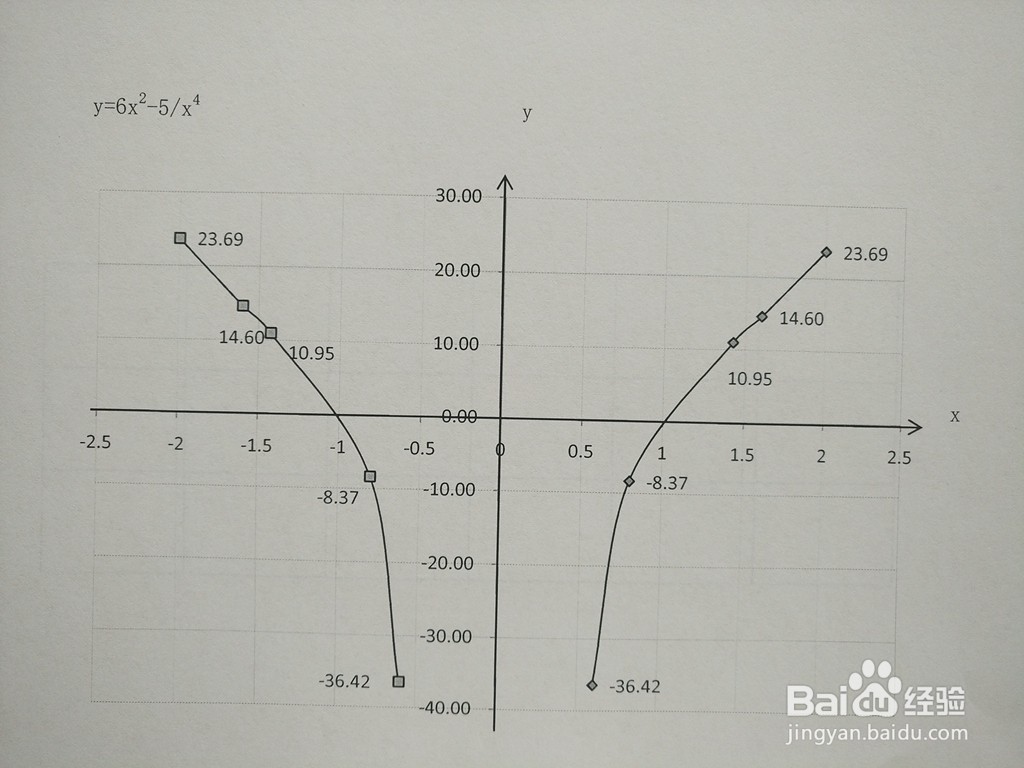
7、通过列表列举函数上部分点示意图如下:。

8、函数极限可以分成 x→0,x→+∞,x→-∞,x→x0 .以 x→x0的极限为例,f(x) 在点 x0以A为极限的定义是: 对于任意给定的正数ε(无论它多么小),总存在正数 A,使得当x满足不等式 0<|x-x0|<δ 时,对应的函数值f(x)都满足不等式:|f(x)-A|<ε ,那么常数A就叫做函数f(x)当 x→x0时的极限。
9、根据函数以上定义域、单调性、凸凹性、极限、奇偶性等性质,可简要在二维坐标系画出示意图。