1、提公因式法:
如果看到多项式中有公因子,先提取一个公因子,将整个问题简化。
例:
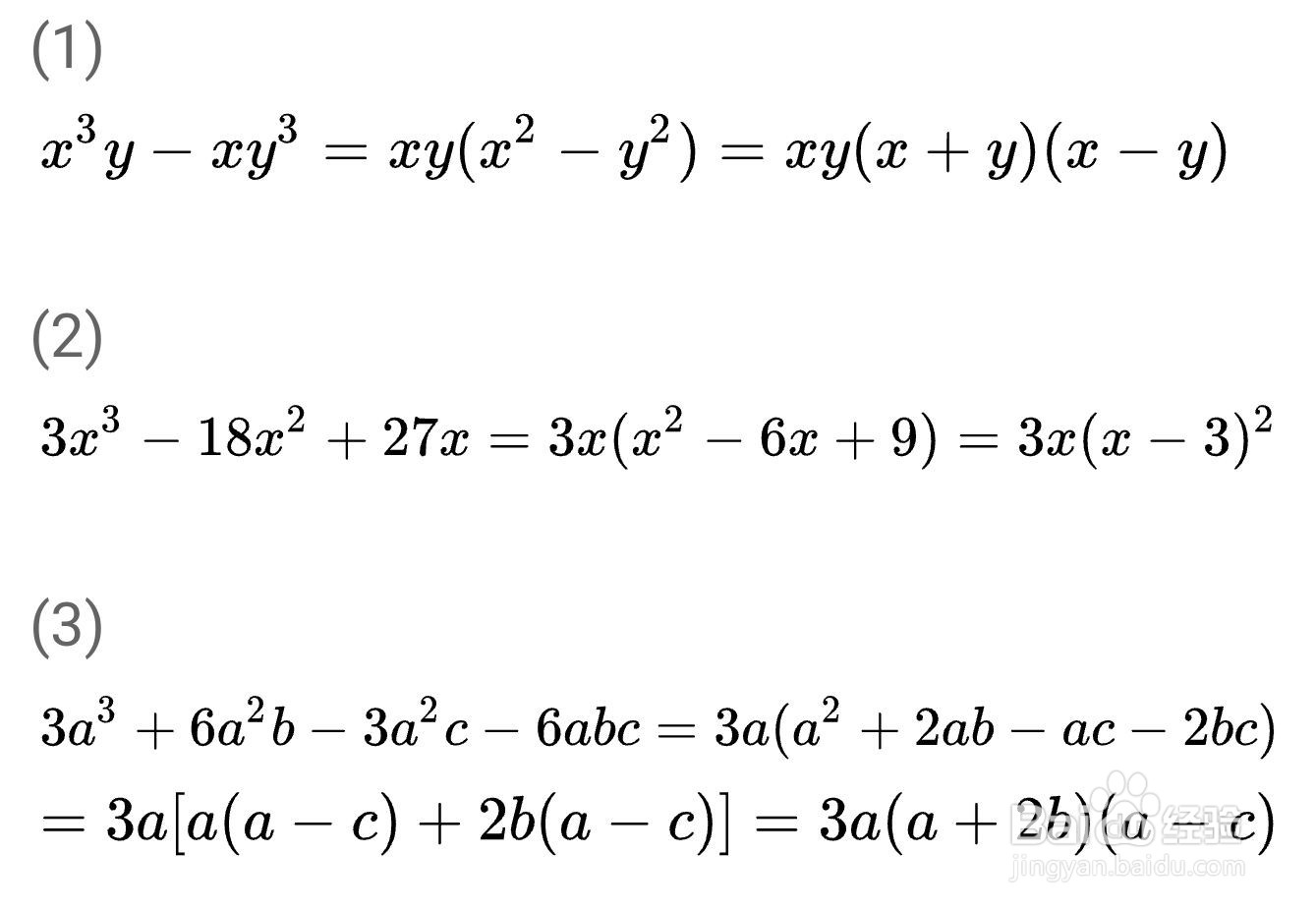
2、公式法:
如果熟悉整式乘积的公式,解决因式分解会变得更快。
再根据公式完成以下例题掌握更快:(a²+b²-1)²-4a²b²。
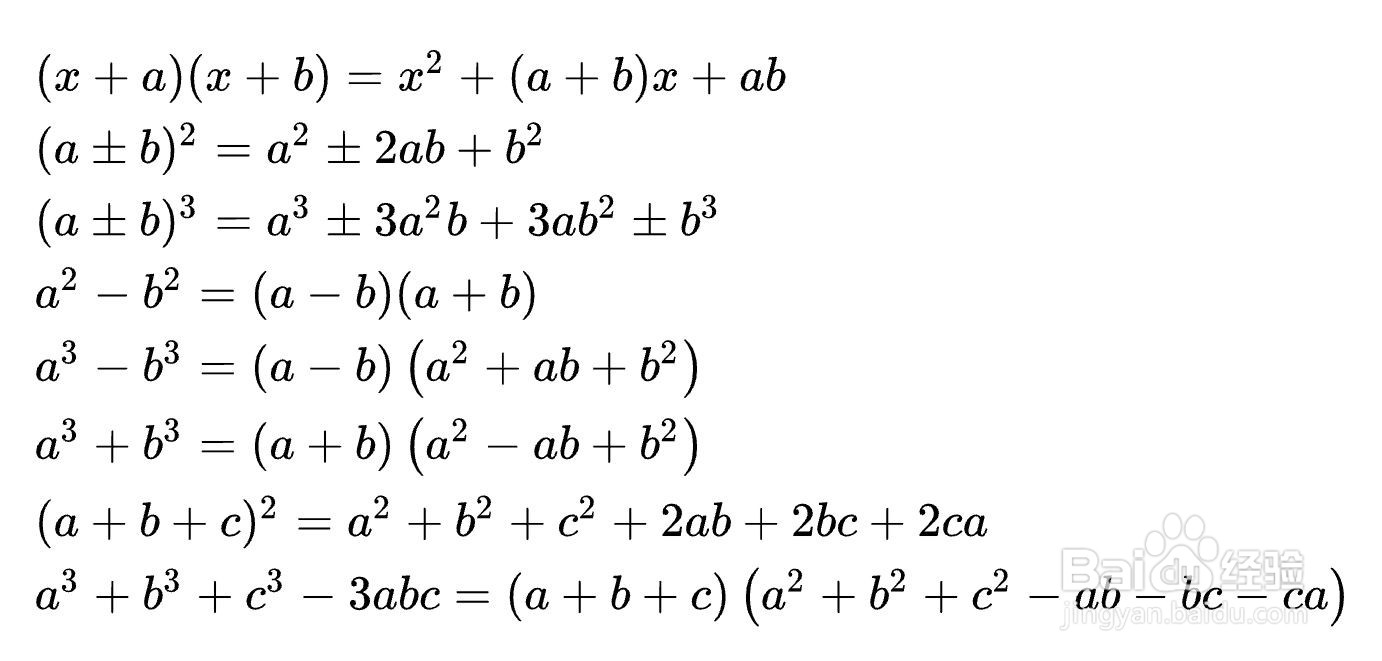

3、十字相乘法:
简单的十字相乘就是公式 (x+a)(x+b)=x²+(a+b)x+ab 的运用。
另附一口诀:首尾分解,交叉相乘,求和凑中。
4、待定系数法:
就是设未知数然后去解方程,比如分解如下多项式: x³-4x²+2x+1 ,是一个一元三次多项式,一般分解肯定是一个一次多项式乘以一个二次多项式,所以不妨设:x³-4x²+2x+1=(x+a)(x²+bx+c)。
如果多项式相等,那么两个多项式每一项前对应的系数相等,所以所以我们就可以得到关于 [公式] 的三个方程,接着求解出来就可以了。 最后可知:x³-4x²+2x+1=(x-1)(x²-3x-1).
5、求根法:若 a 是一元多项式 f(x) 的根,即 f(a)=0 成立,则多项式 f(x) 有一个因式 (x-a) .
6、分组分解法:
是要把多项式进行分组,然后提取出公因子,从而达到因式分解的目的。
