将摆线OBA分成OB段和BA段两段;
用BA段绕y轴旋转所得到的旋转体的体积,减掉 OA段绕y轴旋转得到的旋转体的体积。
O点对刂茗岚羟应的参数t=0,B点对应的参数t=π,A点对应的参数t=2π。
BA段绕y轴旋转所得到的旋转体的体积,从A点的y=0到B点的y=2a,相当于参数t=2π到参数t=π。
OB段绕y轴旋转所得到的旋转体的体积,从O点的y=0到B点的y=2a,相当于参数t=0到参数t=π。
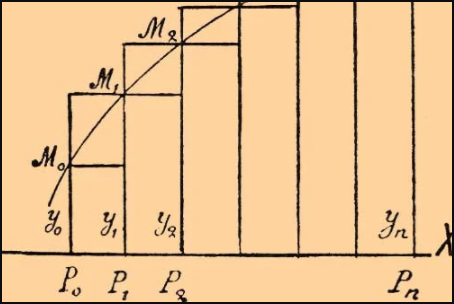
定积分是积分的一种,是函数f(x)在区间[a,b]上积分和的极限。
这里应注意定积分与不定积分之间的关系:若定积分存在,则它是一个具体的数值,而不定积分是一个函数表达式,它们仅仅在数学上有一个计算关系(牛顿-莱布尼茨公式)。
一个函数,可以存在不定积分,而不存在定积分;也可以存在定积分,而不存在不定积分。一个连续函数,一定存在定积分和不定积分;若只有有限个间断点,则定积分存在;若有跳跃间断点,则原函数一定不存在,即不定积分一定不存在。
