根据正态分布的图形来,Φ(X)表示x=X直线的左边的那部分图形的面积,根据对称性,那部分图形关于y轴对称的图形就是x=-X右边那部分图形,那么面积相等,而Φ(-X)表示x=-X左边的那部分图形的面积,由于在整个区间上面积是1,因此Φ(X)+Φ(-X)=1即Φ(-x)=1-Φ(x)。
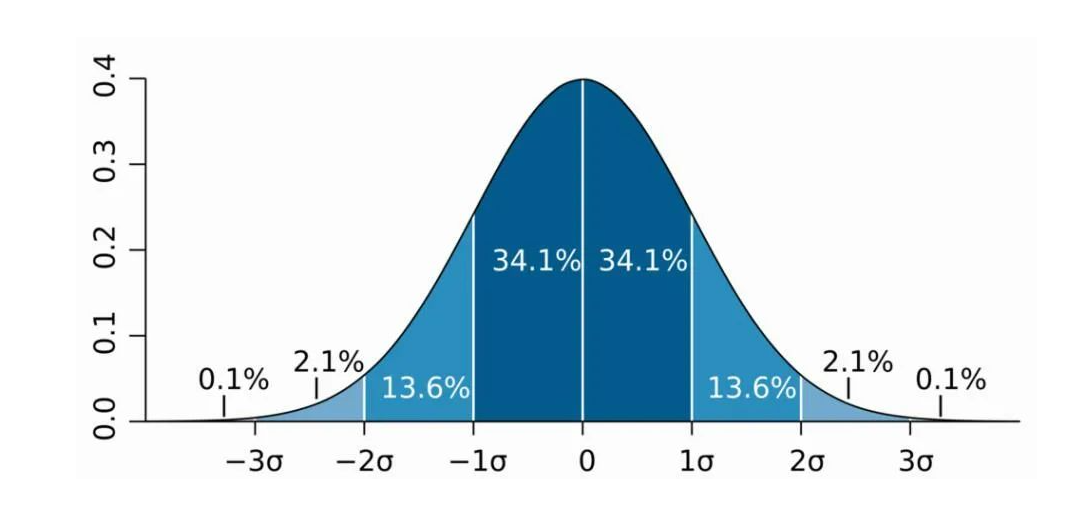
正态分布(Normal distribution),也称“常态分布”,又名高斯分布(Gaussian distribution),是一个非常重要的概率分布。在数学、物理及工程等领域以及统计学的许多方面有着重大的影响力。
正态分布最早由A.棣莫弗在求二项分布的渐进公式中得到。C.F.高斯在研究测量误差时从另一个角度导出了它。P.S.拉普拉斯和高斯研究了它的性质。
